Enough of the math and let's talk about stereos - but don't forget the math. In the digital realm, math also applies where through a combination of sampling rate and the number of bits in the digital word, a numeric value of an analog signal can be stored for that instant in time.
According to the Nyquist theorem, if you store enough samples at a rate that is twice that of human audibility, then a human ear should not be able to tell the difference between the digital reproduction of that analog signal and the original analog signal. In a nutshell, this is how a digital recording works - or not depending upon your point of view and your definition of the word "works."
The compact disk uses 44,100 samples per second (the sampling rate or SR) and a numeric value of that sound pressure in the form of a 16-bit digital number (called a word). From these digital connect-the-dot approximations, we get very low noise and pretty good quality simulations of what the original analog signal originally was.
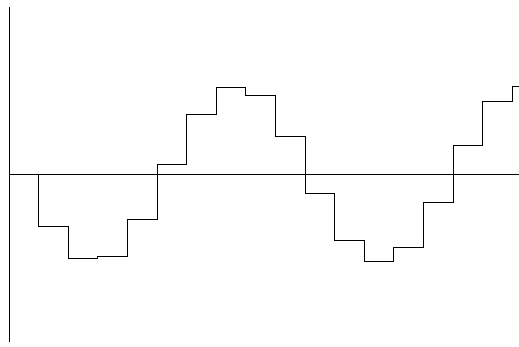 |
| Low Digital Sampling Rate |
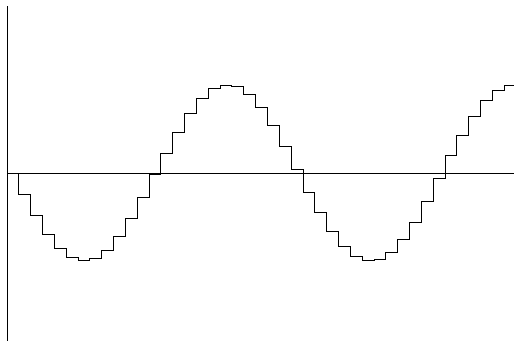 |
| High digital Sampling Rate |
The trend in the high-end audio realm is to get better resolution recordings since this pretty good 44/16 standard leaves a little to be desired (dots are a little too far apart). Getting back to the math for an instant, this means that the value of X is 44,100 so the value of Y is again pretty small (about 0.0000022676 or 2.2676 times 10 to the minus 5th power written for short as 2.2676e-5). Recent digital recordings do two things to improve this resolution: increase the sampling rate and increase the size of the digital word. Several standards are now being used, the most popular being 192/24 meaning that the SR=192,000.
Again referring back to the math, this means that the value of Y is even smaller (about 0.00000052083 or 5.2083e-6). So what this means it that as the sampling rate approaches zero, the resolution of the analog reproduced version gets more accurate. If we were to make the SR larger still, the value of Y would get even smaller.
If the SR=infinity, then the digitally stored version would be equal to the analog original, right? So at a value of infinity, the value of Y=0 or Y=1/infinity.
Let's look at this simple equation in a little more detail from the mathematical point of view ignoring Nyquist and his theory for the moment, and see what it is telling us.
At a SR=infinity, the numerically stored signal is absolutely identical to that of the original; anything less than infinity is close, but no cigar. So what this is alluding to is that an analog original signal is the same thing as numerical infinity, right? And any attempt at a digital copy falls short of this regardless of how high the finite sampling rate. So an analog recording is effect a digital recording with an infinite number of samples. BTW, this same argument applies to comparing pure Class A amplifiers and other Classes of amplifiers (B, AB, D, etc.).
When you look at the grooves of an analog vinyl disc, you are looking at what an infinite digital sampling rate is; perfectly sinusoidal with no straight-line connect-the-dots approximation.
 |
| Infinite Digital Sampling Rate |
Yours for higher fidelity,
Philip Rastocny
Philip Rastocny
I do not use ads in this blog to help support my efforts. If you like what you are reading, please remember to reciprocate, My newest title is called Where, oh Where did the Star of Bethlehem Go? It’s an astronomer’s look at what this celestial object may have been, who the "Wise Men" were, and where they came from. Written in an investigative journalism style, it targets one star that has never been considered before and builds a solid case for its candidacy.
- Althea: A Story of Love
- Build an Extreme Green Composter
- The Extreem Green Guide to Wind Turbines
- Build and Extreme Green Hot Water Solar Collector
- The Extreme Green Guide to Solar Electricity
- The Extreme Green Guide to Improving Mileage
- Meditation for Geeks (and other left-brained people)
- Build an Extreme Green Raised Bed Garden
- Build an Extreme Green Rain Barrel
- Build an Extreme Green Squirrel-Proof Bird Feeder
- Extreme Audio 1: House Wiring
- Extreme Audio 2: Line Filtering
- Extreme Audio 3: Chassis Leakage
- Extreme Audio 4: Interconnect Cables
- Extreme Audio 5: Speaker Wires
- Extreme Green Organic Gardening
- Extreme Green Organic Gardening 2012
- The Extreme Green Appliance Buying Guide

No comments:
Post a Comment
To comment on this blog, you must first be a member. All comments are moderated.
Note: Only a member of this blog may post a comment.